ここで、メートルねじのねじ山について、これまでにも出てきたいくつかの
寸法と規格を、断面図を見ながら確認しておきましょう。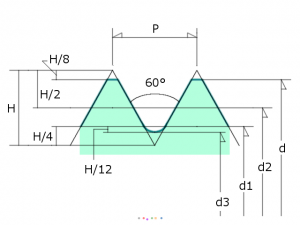
上の図は基準寸法を表しています。
山谷の角度が 60°なので仮想三角形の高さ H はねじ山の
ピッチ P から決まります（H=P√3/2）。
図の左半分、全ての高さ寸法の割合は、この H に対する比率で定められています。
d（ねじの呼び＝最外径＝直径）からこれらの高さ寸法を差し引いた値、
d1、d2、d3 は、耐荷重の計算や加工の目安に用いられます。
すなわち、ねじ山の全ての基準寸法は、呼び d とピッチ P
（ねじを選択するときに必ず必要な2つの値）のみによって決められているということです。
- P：ねじ山のピッチ
- H：仮想三角形の高さ
- d：ねじの呼び＝最外径（直径）
d2 と d3 は、例えば有効断面積にその値が用いられます。
有効断面積 As は、d2 と d3 の平均を直径とした円の面積です。
As = (π/4)*{(d2+d3)/2}^2
d2 も d3 も d と P とで決まるので（上図）、同じ式を d と P だけで表すこともできます。
As = 0.7854*(d-0.9382P)^2
【一般用メートルねじの呼びと有効断面積（M1からM10）】
（JIS B 0205-3:2001にて推奨される選択のみ抜粋）
| 呼び | ピッチ mm | 有効断面積 mm^2 |
|---|---|---|
| M1 | 0.25 | 0.460 |
| M1.2 | 0.25 | 0.732 |
| M1.4 | 0.3 | 0.983 |
| M1.6 | 0.35 | 1.27 |
| M1.8 | 0.35 | 1.70 |
| M2 | 0.4 | 2.07 |
| M2.5 | 0.45 | 3.39 |
| M3 | 0.5 | 5.03 |
| M3.5 | 0.6 | 6.78 |
| M4 | 0.7 | 8.78 |
| M5 | 0.8 | 14.2 |
| M6 | 1 | 20.1 |
| M7 | 1 | 28.9 |
| M8 | 1.25 | 36.6 |
| M8 | 1 | 39.2 |
| M10 | 1.5 | 58.0 |
| M10 | 1.25 | 61.2 |
| M10 | 1 | 64.5 |
おねじとめねじの基準寸法は同じです（第3節の表を参照）。
したがって公差ゼロで作ってしまうとこれらはうまく噛み合いません。
先の節でも出てきましたが、おねじもめねじも、公差ゼロから一方的に
離れる方向の「公差域」をもって造られています。
公差域は、基準寸法からのオフセットである公差位置と、
公差の幅である公差グレードとの組み合わせによって表されます。
- 公差位置
アルファベットの G, H, e, g, h でオフセットを表します。
例えばおねじのh、めねじのHは共に公差0から、
それぞれが離れる方向に幅を持ちます。 - 公差グレード（幅）
4,5,6 など、数値をグレードとして公差の幅を表します。
